円と関数の関係

問題１６

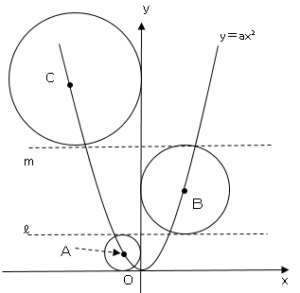
図のように関数$y=ax²$のグラフ上の点$A,B,C$を中心とする$3$つの円がある。直線$ℓ,m$は$x$軸に平行で、点$A$を中心とする円は$x$軸、$y$軸、直線$ℓ$に、点$B$を中心とする円は$y$軸、直線$ℓ,m$に、点$C$を中心とする円は$y$軸,直線$m$にそれぞれ接しており、点$A$の座標は$(-1,1)$とする。
ア、$a$の値を求めよ。
イ、点$B$の座標を求めよ。
ウ、$3$点$A,B,C$を通る円の半径を求めよ。

ア、
$y=ax²$上に点$A$の座標を代入して、
$1=a×(-1)²$
$a=1$

イ、


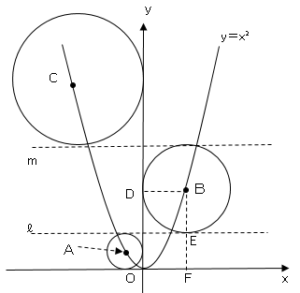
図のように点$D,E,F$をおく。
点$B$の$x$座標を$b$とすると、$DB=BE$より、$BE=b$となる。
点$A$を中心とする円の直径は$2$より、$EF$の長さは$2$これより、点$B$の$y$座標は
$BE+EF$
$=b+2$

点Bの座標は$y=x²$のグラフ上なので、
$b+2=b²$
$b²-b-2=0$
$(b-2)(b+1)=0$
$b=2,-1$
$B$の$x$座標は正なので、点$B(2,4)$

ウ、
イ、と同様に点$C$を求める。
点$C$の$x$座標を$-c$とすると$y$座標は$c+6$
$(c+6)=(-c)²$
$c²-c-6=0$
$(c-3)(c+2)=0$
$c=3,-2$
$c>0$より$c=3$となる。よって点$C$の座標は$(-3,9)$


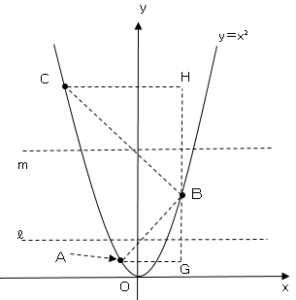
$AG$の長さは$2-(-1)=3$、$BG$の長さは$4-1=3$
これより△$ABG$は$1:1:\sqrt{2}$の三角形であり、∠$ABG=45°$･･･①

また$CH$の長さは$2-(-3)=5$、$BH$の長さは$9-4=5$
これより△$BCH$は$1:1:\sqrt{2}$の三角形であり、∠$CBG=45°$･･･②

①,②より、∠$ABC=90°$これより直線$AC$は円の直径となる。

よって半径は$AC$の長さの半分になる。
$AC=\sqrt{(-3-(-1))²+(9-1)²}$
$AC=\sqrt{4+64}$
$AC=2\sqrt{17}$
よって半径は$\sqrt{17}$