関数と文章問題

問題２

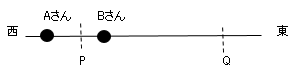
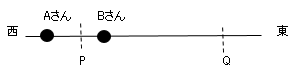
東西にのびるまっすぐな道路上に地点$P,Q$がある。
$A$さんは地点$Q$に向かって、この道路の地点$P$より西を秒速$3m$で走っていた。
$B$さんは地点$P$に止まっていたが、$A$さんが地点$P$に到着する直前に、この道路を地点$Q$に向かって自転車で出発した。
$B$さんは地点$P$から出発してから$8$秒間はしだいに速さを増していき、その後は一定の速度で走り、$12$秒後に地点$Q$に到着した。
$B$さんが地点$P$から出発してから$x$秒間に進む距離を$ym$とすると、$x$と$y$の関係は表のようになります。

$0≦x≦8$では$x$と$y$の関係は$y=ax²$で表せる。
1.$a$の値を求めなさい。
2.表のア,イを埋めなさい。
3.$x$の変域が$8≦x≦12$のとき、$y$を$x$の式で表しなさい。
4.$x$と$y$の関係をグラフに表しなさい。
5.$B$さんは地点$P$を出発してから、$2$秒後に$A$さんに追いつかれた。
(ア)$B$さんが地点$P$を出発したとき、$A$さんと$B$さんの距離は何$m$でしたか。
(イ)$B$さんは地点$P$を出発し、$A$さんに追いつかれたが、その後再び追いついた。それは$P$を出発してから何秒後か。

1.
図より、$x=8$のとき$y=16$となる。
$y=ax²$に代入して
$16=a×(8)²$
$64a=16$
$a=\displaystyle \frac{1}{4}$

2.
$y=\displaystyle \frac{x²}{4}$に$y=4$を代入して
$4=\displaystyle \frac{x²}{4}$
$16=x²$
$x=4(0≦x≦8)$
また、$8$秒以降は一定の速さで走るので、比例の関係になっていることがわかる。
図より$2$秒間で$8m$進んでいるので、更に$2$秒後の$12$秒では$32m$進む。

3.
2.より比例関係になっているので$y=4x-16$となる。

4.
グラフは以下


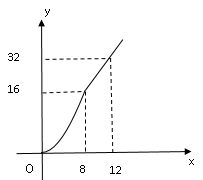
5.
ア、
$2$秒後に進む距離はそれぞれ$A$さんは$3×2$で$6m$,$B$さんは$y=\displaystyle \frac{x²}{4}$に$x=2$を代入して$y=1$つまり$6-1$の$5m$の差があった。
イ、
$A$さんの速さは$3(m/s)$で、$5m$の差があることから$y=3x-5$と表すことができる。
グラフに記入すると$B$さんは$A$さんに追いついた。その後に追い抜かしていることがわかる。

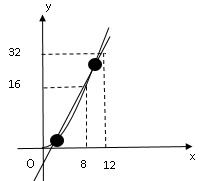
その交点を求める。
$3x-5=4x-16$
$-x=-11$
$x=11$なので$11$秒後に再び追いついた。