平行を利用した相似の証明問題と辺の比の問題
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
5989 Views
問題11図のように、平行四辺形ABCDがある。辺ABの中点をEとし、点Eを通り線分BDに平行な直線と辺ADとの交点をFとする。また、線分CFと線分ED、BDとの交点をそれぞれG,Hとする。
(1)△AEF∽△ABDを証明しなさい。
(2)CH:HGを最も簡単な整数比で表しなさい。
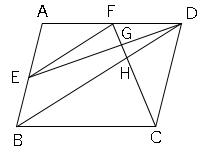
(1)△AEF∽△ABDを証明しなさい。
(2)CH:HGを最も簡単な整数比で表しなさい。

方針
平行の特徴を考えると同位角・錯角が見えてくる。
(1)平行の特徴を考える
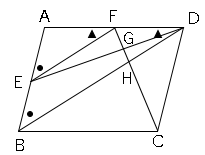
(1)△AEFと△ABDにおいて、
EF//BDより、同位角が等しいので、
∠AEF=∠ABD・・・➀
∠AFE=∠ADB・・・➁
➀、➁より2角がそれぞれ等しいので、
△AEF∽△ABD
(2)平行四辺形なので角を頼りに相似な三角形を探す
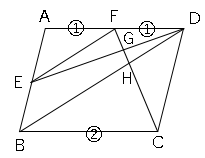
$AF:FD=1:1$より、
$FD:BC=1:2$
△FHD∽△CHBより
$FH:CH=FD:CB=HD:HB=1:2$
また(1)より△AEF∽△ABDなので、
$EF:BD=1:2$
$EF:3=1:2$
$EF=\displaystyle \frac{3}{2}$
△EGF∽△DGHより
$FG:HG=EF:DH$
$FG:HG=\displaystyle \frac{3}{2}:1$
$FG:HG=3:2$
これより
$HF:HG=5:2$
$HF=\displaystyle \frac{5}{2}HG$
ゆえに
$CH:HF=2:1$
$CH:\displaystyle \frac{5}{2}HG=2:1$
$CH:HG=5:1$
不明点があればコメント欄よりお願いします。







ディスカッション
コメント一覧
EF:3=1:2の3が何か分かりません。
HD:HB=1:2
だからBD=3になるよ。