円が２つある相似の証明問題と面積を求める問題

問題９図のように、線分ＡＢを直径とする円Ｏと直線ℓがあり、ℓは点Ｂで円Ｏに接している。円Ｏの円周上に点Ｃをとり、△ＡＢＣをつくる。直線ＡＣとℓとの交点をＤとする。

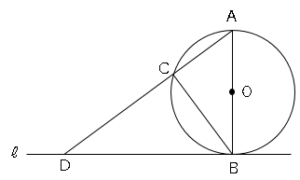
（１）∠ＡＣＢの大きさを求めなさい。
（２）△ＡＢＣ∽△ＡＤＢを証明しなさい。
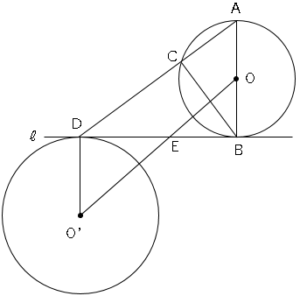
（３）図２は図１において、点Dでℓに接する円Ｏ’を書いたものである。線分ＯＯ’をひき、ℓとＯＯ’との交点をＥとする。ＯＯ’＝５ｃｍ、円Ｏ、Ｏ’の半径をそれぞれ１ｃｍ、２ｃｍとするとき、線分ＤＥの長さを求めなさい。

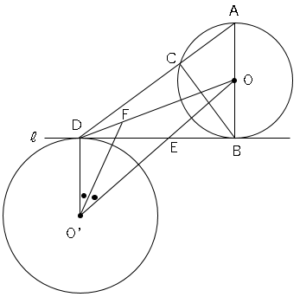
（４）図の３は、図２において、線分ＤＯをひいたものである。∠ＤＯ’Ｏの二等分線とＤＯとの交点をＦとするとき、△ＤＯ’Ｆの面積を求めなさい。

方針

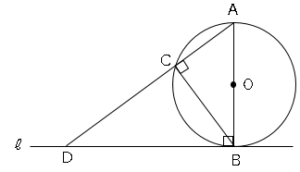
（１）円周角の定理より、∠ＡＣＢ＝９０°
△ＡＢＣと△ＡＤＢにおいて、
接線と円の関係より∠ＡＢＤ＝９０°
（１）より∠ＡＣＢ＝９０°
なので∠ＡＣＢ＝∠ＡＢＤ・・・➀
∠Ａは共通・・・➁
➀、➁より２角がそれぞれ等しいので、
△ＡＢＣ∽△ＡＤＢ

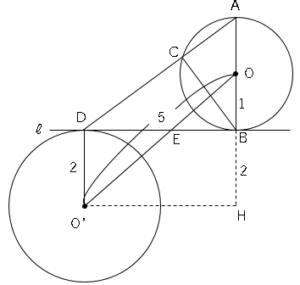
図のように補助線（垂線）を引き、Ｈを置く。△ＯＨＯ’に三平方の定理を用いて、Ｏ’Ｈ＝４ｃｍ
また、△ＯＢＥ∽△ＯＨＯ’（２角が等しい）ので、ＢＥの長さは
$OB:OH=BE:HO’$
$1:3=BE:4$
$BE=\displaystyle \frac{4}{3}$

よってＤＥの長さは
$DE=4-\displaystyle \frac{4}{3}$
$DE=\displaystyle \frac{8}{3}$

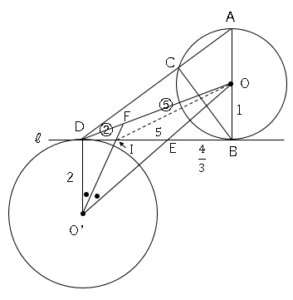
図のようにＩを置き、ＩＯを結ぶ。
△ＤＯ’Ｆ＝△ＤＩＯ’＋△ＤＩＦで考える

△ＤＩＦを求める。
角の２等分線より、
$DF:FO=O’D:O’O$
$DF:FO=2:5$

Ｏ’Ｅの長さは三平方の定理より、
$O’E²=O’D²+DE²$
$O’E²=4+\displaystyle \frac{64}{9}$
$O’E=\displaystyle \frac{10}{3}$

先ほどと同様に角の２等分線より、
$DI:IE=O’D:O’E$
$DI:IE=2:\displaystyle \frac{10}{3}$
$DI:IE=3:5$

これよりＩＥの長さは
$IE=\displaystyle \frac{5}{8}×DE$
$IE=\displaystyle \frac{5}{8}×\displaystyle \frac{8}{3}$
$IE=\displaystyle \frac{5}{3}$

これより△ＤＩＦの面積は
△$DIF=\displaystyle \frac{2}{7}$△$DIO$
△$DIO=\displaystyle \frac{3}{5}$△$OIE$

ゆえに
△$DIF=\displaystyle \frac{2}{7}×\displaystyle \frac{3}{5}$△OED
△$DIF=\displaystyle \frac{6}{35}×\displaystyle \frac{5}{3}×1÷2$
△$DIF=\displaystyle \frac{1}{7}$

△ＤＩＯ’を求める。
△$DIO’=2×1÷2$
△$DIO’=1$

これより求める面積は
△$DO’F=1+\displaystyle \frac{1}{7}$
△$DO’F=\displaystyle \frac{8}{7}$