距離と作図
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
4457 Views
問題１２
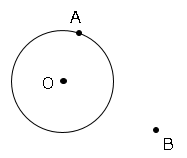
図のように、点Ｏを中心とする円の周上に点Ａがあり、円の外部に点Ｂがある。Ａを接点とする円Ｏの接線上にあって、２つの線分ＯＰ,ＰＢの長さが最小になる点Ｐを作図せよ。
図のように、点Ｏを中心とする円の周上に点Ａがあり、円の外部に点Ｂがある。Ａを接点とする円Ｏの接線上にあって、２つの線分ＯＰ,ＰＢの長さが最小になる点Ｐを作図せよ。
方針最終的に求める点を作図してから、何をすればいいか考える。
まず接線を引き、点Ｐを作図する。
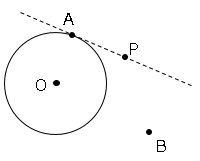
線分ＯＰ、ＢＰを引く。
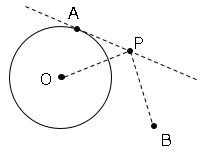
線分ＯＰ,ＰＢの長さが最小になるには円Ｏを直線ＡＰに対して対象移動させる。
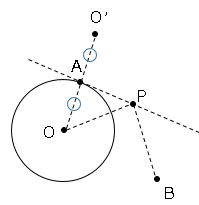
点Ｏ’から点Ｂを引けばＰが求まる。
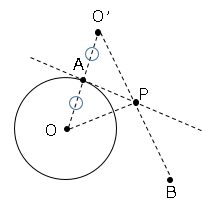
まず接線を引き、点Ｐを作図する。
線分ＯＰ、ＢＰを引く。
線分ＯＰ,ＰＢの長さが最小になるには円Ｏを直線ＡＰに対して対象移動させる。
点Ｏ’から点Ｂを引けばＰが求まる。
➀半直線ＯＡを引き、垂直二等分線を引く。
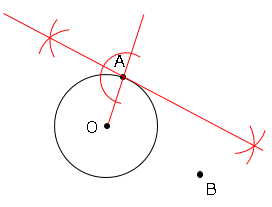
➁線分ＯＡを半径とする円と半直線ＯＡの交点を求める。
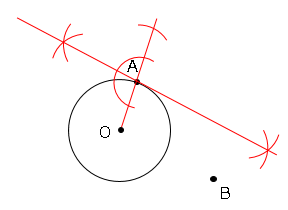
➂➁で求めた交点とＢを結び、接線との交点をＰとする。
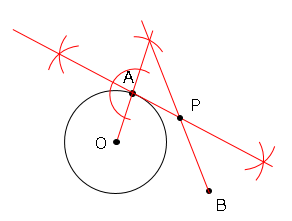
不明点があればコメント欄よりお願いします。