特徴を持つ三角形の証明
オンライン塾始めました。
６ヶ月で自分で勉強できるようにサポートします。
5228 Views
二等辺三角形の特徴
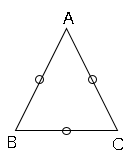
２つの辺が等しい三角形を二等辺三角形といいます。
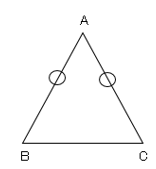
二等辺三角形ならば、底角が等しいことになります。
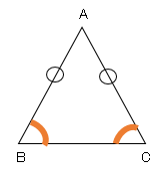
二等辺三角形の頂角の二等分線は、底辺を二等分します。
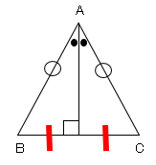
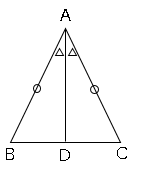
では問題です。二等辺三角形の頂角の二等分線は、底辺を垂直に2等分することを証明しましょう。
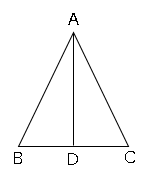
正三角形の特徴
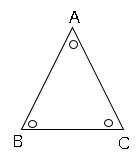
３つの辺が等しい三角形を正三角形といいます。
正三角形ならば、１つの角は$60°$となります。
では問題です。△$ABC$で∠$A$＝∠$B$＝∠$C$ならば、$AB$＝$BC$＝$CA$を証明しましょう。
直角三角形の合同条件
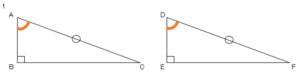
２つの条件があります。
１,斜辺と$1$つの鋭角がそれぞれ等しい。
２,斜辺とその他の辺がそれぞれ等しい。
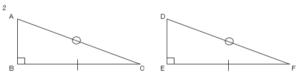
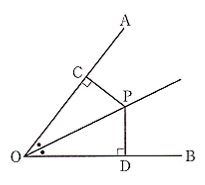
では問題です。図のように、∠$AOB$の二等分線上の１点を$P$とし、$P$から$OA$,$OB$に垂線をひき、$OA$,$OB$との交点をそれぞれ$C,D$とする。このとき、$CP=DP$であることを証明しなさい。
不明点があればコメントよりどうぞ。