式の展開と因数分解の練習問題２
LINE@始めました。
友達追加をよろしくお願い申し上げます。
勉強のやり方の相談・問題の解説随時募集しています！
お気軽にＬＩＮＥしてください。
2544 Views
2019年3月16日式の展開と因数分解中学３年生
問１
$x+y=-1$,$xy=-6$のとき、$(x-y)²$の値を求めましょう。
（１）
ポイントは
「無理やり作ること」
$(x-y)²$
$=x²-2xy+y²$
$=x²+y²+12$
$=(x+y)²-2xy+12$
$=(-1)²+12+12$
$=25$
問２
図の四角形$ABCD,BEFG$は、$1$辺がそれぞれ$a,b$の正方形で、$M$は$AE$の中点である。ただし$a>b$とする。
$AM,MB$をそれぞれ$1$辺とする$2$つの正方形の面積の和は、正方形$ABCD,BEFG$の面積の和の半分に等しいことを証明しましょう。
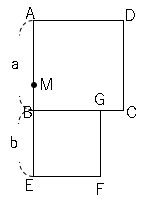
$AM$の長さは$\displaystyle \frac{a+b}{2}$
$MB$の長さは
$a-\displaystyle \frac{a+b}{2}$
$=\displaystyle \frac{a-b}{2}$
これより
$AM,MB$をそれぞれ$1$辺とする$2$つの正方形の面積の和は
$(\displaystyle \frac{a+b}{2})²$+$(\displaystyle \frac{a-b}{2})²$
$=\displaystyle \frac{a²+2ab+b²}{4}+\displaystyle \frac{a²-2ab+b²}{4}$
$=\displaystyle \frac{2a²+2b²}{4}$
$=\displaystyle \frac{a²+b²}{2}$
ゆえに
正方形$ABCD,BEFG$の面積の和$(a²+b²)$の半分に等しい。
動画で理解しよう！ここまでの内容だよ
不明点があればコメントよりどうぞ。