空間図形の練習問題2
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
4938 Views
2018年3月16日空間図形中学1年生
問1
図の直線ℓを軸として1回転させた立体の体積を求めましょう。
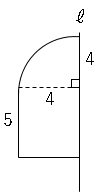
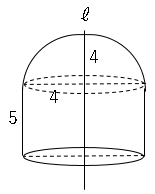
半球と円柱の体積の和が求める体積となる。
半球の体積$=\displaystyle \frac{4}{3}×π×4³$$×\displaystyle \frac{1}{2}$
半球の体積$=\displaystyle \frac{128}{3}πcm³$
円柱の体積$=4×4×π×5$
円柱の体積$=80πcm³$
求める体積は
$=\displaystyle \frac{128}{3}π+80π$
$=\displaystyle \frac{368}{3}πcm³$

問2
1辺が$12cm$の正方形$ABCD$で、辺$AB,AD$上の中点をそれぞれ$M,N$とする。線分$MN,MC,CN$を折り目として折り曲げ、3点$A,B,D$を1点に重ねて立体を作る。
(1)立体の体積を求めましょう。
(2)△$MCN$を底面とした場合、立体の高さを求めましょう。
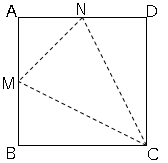
(1)
図のようにわかるところを書く。
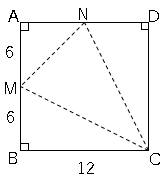
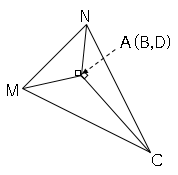
すると体積は底面が△AMNで高さがBCの三角錐となるので、
$=6×6×\displaystyle \frac{1}{2}×12×\displaystyle \frac{1}{3}$
$=$
$72cm³$
(2)
底面は正方形から3つの三角形を引くと求まる。
それぞれ求めると、
正方形の面積$=12×12$
正方形の面積$=144cm²$
△$AMN$の面積$=6×6×\displaystyle \frac{1}{2}$
△$AMN$の面積$=18cm²$
△$MBC$の面積$=6×12×\displaystyle \frac{1}{2}$
△$MBC$の面積$=36cm²$
△$MBC$と△$CND$は同じ面積
よって
△$MNC$の面積$=144-18-36-36$
△$MNC$の面積$=54cm²$
(1)より体積は求まっているから高さ$h$とすると、
$54×h×\displaystyle \frac{1}{3}=72$
$18×h=72$
$h=4cm$

問3
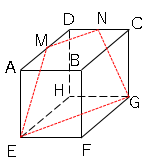
図の立体を次のような平面で切った場合の切り口はどのような図形になっていますか?
(1)平面$ACF$
(2)平面$ADFG$
(3)辺$AD$の中点$M$,辺$DC$の中点$N$とするとき、平面$MNEG$
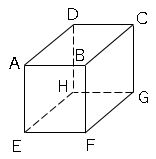
コツは包丁で豆腐を切るイメージを持つとわかりやすくなります。
実際に切ってみましょう。
(1)
三角形
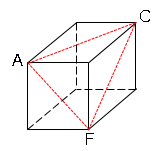
(2)
長方形
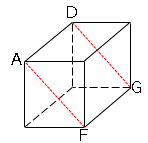
(3)
台形

不明点があればコメントよりどうぞ。



















ディスカッション
コメント一覧
まだ、コメントがありません