2次方程式の利用
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
2393 Views
2019年3月16日2次方程式中学3年生
2次方程式の利用
ポイントは2つあり、
・わからないものや求めたいものを文字$x$などで置き換える。
・等しい関係を見つけて、2次方程式を作る。
例
大小$2$つの正の数がある、その差は$6$で、積は$40$になる。このときの$2$数を求めよ。
大きい方の数を$x$と置くと、小さい方の数は$x-6$となる。
この$2$つの積が$40$なので、
$x(x-6)=40$
$x²-6x-40=0$
$(x-10)(x+4)=0$
$x=10,-4$
大小$2$つの正の数なので、$2$数は$10,4$
では問題です。周の長さが$40cm$で面積が$80cm²$の長方形を作る。このときの縦と横の長さを求めよ。縦の長さの方が横の長さよりも長いとする。

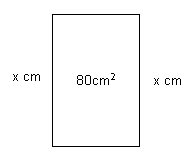
ポイントは
縦の長さを文字で置くと周りの長さから、横の長さが出せる。
縦の長さを$x$とすると、横の長さは$2($縦の長さ$+$横の長さ$)=$周の長さ
$2(x+$横の長さ$)=40$
$x+$横の長さ$=20$
横の長さ$=20-x$
となる。
また、面積が$80cm²$なので、
$x(20-x)=80$
$20x-x²-80=0$
$x²-20x+80=0$
解の公式より
$x=\displaystyle \frac{-(-20)±\sqrt{(-20)²-4×1×80}}{2×1}$
$x=\displaystyle \frac{20±\sqrt{80}}{2}$
$x=\displaystyle \frac{20±4\sqrt{5}}{2}$
$x=10±2\sqrt{5}$
縦の長さが横よりも長いので、
$x=10+2\sqrt{5}$
横の長さは
$20-(10+2\sqrt{5})$
$=10-2\sqrt{5}$
よって
長方形の縦と横の長さは$x=10+2\sqrt{5}$と$10-2\sqrt{5}$
更に問題です。$1$辺が$9cm$の正方形がある。
点$P$は、辺$AB$上を毎秒$1cm$で$A$から$B$まで、点$Q$は、辺$BC$上を毎秒$1cm$で$B$から$C$まで動く。
△$PQB$の面積が$10cm²$となるのは何秒後ですか。
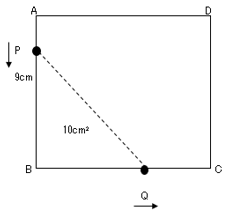
$x$秒後の$PB$の長さは$(9-x)cm$、
$BQ$の長さは$xcm$
よって
$x(9-x)÷2=10$
$9x-x²=20$
$-x²+9x-20=0$
$x²-9x+20=0$
$(x-4)(x-5)=0$
$x=4,5$
よって$4$,$5$何秒後
更に問題です。
点$P$は$y=x+3$上にあり、点$Q$は点$P$より$x$軸に垂線を下ろしたときの$x$軸との交点である。
△$POQ$の面積が$14cm²$のとき点$P$の座標を求めなさい。
点$P$の$x$座標は正で、座標軸の$1$目盛りは$1cm$とする。

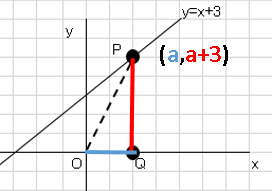
点$P$の$x$座標を$a$とすると、点$P$の$y$座標は$a+3$となる。
よって
$a(a+3)÷2=14$
$a²+3a-28=0$
$(a+7)(a-4)=0$
$a=-7,4$
点$P$の$x$座標は正より
$a=4$
点$P$は$(4,7)$
動画で理解しよう!ここまでの内容だよ


不明点があればコメントよりどうぞ。














ディスカッション
コメント一覧
まだ、コメントがありません