二次関数とグラフ
オンライン塾始めました。
6ヶ月で自分で勉強できるようにサポートします。
二次関数
$2$乗に比例する関数$x$と$y$の関係が、$y=ax²$で表されるとき、$y$は$x$の$2$乗に比例する(二次関数となる)。
※$a≠0$,$a$は比例定数
性質:$x$の値が$2$倍,$3$倍・・・$n$倍となると、$y$の値は$2²$倍,$3²$倍・・・$n²$倍となっていく。

では問題です。関数$y=5x²$について、以下の問いに答えましょう。
(1)$x=2$のときの$y$の値
(2)$y=2$のときの$x$の値
さらに問題です。$y$を$x$の式で表しましょう。また、それぞれについて、$x=-4$のときの$y$の値を求めましょう。
(1)$y$は$x$の2乗に比例し、$x=2$のとき$y=12$である。
(2)関数$y=ax²$で、$x=3$のとき$y=-9$である。
二次関数のグラフの作成
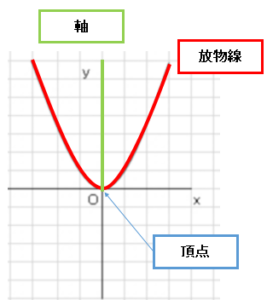
図のような放物線が二次関数のグラフになります。軸と放物線の交点を頂点と言います。対称の軸を放物線の軸といいます。
では$y=2x²$のグラフを書いてみよう。
➀表を書く
②点を書き写す
③線で結ぶ
➀表を書く
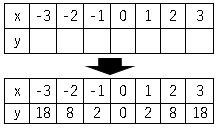
②点を書き写す
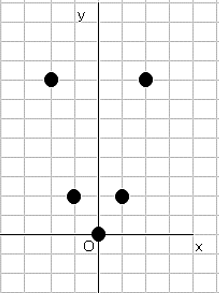
③線で結ぶ
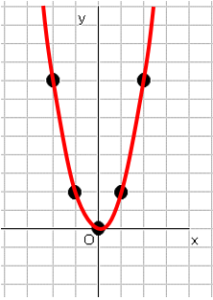

問題です。$y=\displaystyle \frac{1}{2}x²$のグラフを書きましょう。
二次関数と変域
$y=2x²(-1≦x≦2)$のとき$y$の変域を考えましょう。
必ず図を書いて考えます。
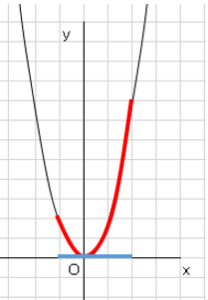
$0≦y≦8$
※$y$の変域は$0$を通っていることに注意してください。
では問題です。$y=x²(-3≦x≦1)$のときの$y$の変域を求めなさい。
変化の割合と増加量
変化の割合とは傾きのことである。
変化の割合$=\displaystyle \frac{yの増加量}{xの増加量}$$=\displaystyle \frac{まで-から}{まで-から}$

では問題です。関数$y=\displaystyle \frac{1}{4}x²$について、$x$の値が$4$から$8$まで増加するときの変化の割合を求めましょう。
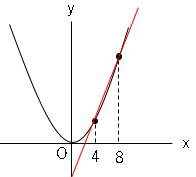









ディスカッション
コメント一覧
まだ、コメントがありません